De fleste har nok stået og funderet over, hvordan man udstikker sine småkager, så mindst muligt dej går til spilde. Men nu har selv matematiske eksperter opgivet at finde en computeralgoritme, der kan give svaret på den slags geometriske problemer.

Hvordan bruger vi mest muligt af dejen, når vi stikker småkager ud til jul? Og hvordan pakker vi kufferten og køkkenskabet, så vi udnytter pladsen bedst muligt? Der må være en måde, der er mest optimal, har mange sikkert tænkt i sådanne situationer. Men det er spild af tid at gruble over den slags spørgsmål, for videnskaben har nu påvist, at det er umuligt at regne ud på nuværende tidspunkt – i hvert fald hvis det drejer sig om mere end fire-fem klejner eller peberkagemænd.
Det er adjunkt Mikkel Abrahamsen fra Datalogisk Institut, som sammen med to forskerkolleger har undersøgt, hvor svært det er at regne sig frem til den mest optimale måde at pakke objekter på i to dimensioner uden overlap – en gåde, som har optaget dataloger i årtier.
“Selvom vi er i stand til at løse ret komplekse problemer ved hjælp af algoritmer, er dette problem åbenbart stadig for stor en mundfuld for de computere, der findes i dag. På nuværende tidspunkt er det ikke muligt at pakke mere end 5-10 objekter optimalt, og vores resultat indikerer, at det tal nok ikke kommer til at stige ret meget lige foreløbig,” siger Mikkel Abrahamsen.
At pakke ting på den mest optimale måde kan ikke kun være et problem derhjemme, men også i mange industrier. Det gælder fx i tøjproduktion og metalforarbejdning, når man forsøger at skære materialer ud, så mindst muligt går til spilde, og i shippingbranchen når man pakker containerne.
Højst fire klejner
Man kender i dag størrelsen på den mindste kvadratiske container, hvor man kan pakke op til 10 kvadratiske paller på 1×1 meter. Men hvis man tilføjer bare én ekstra palle, kan man ikke regne den optimale størrelse på containeren ud, fortæller Mikkel Abrahamsen.
“Beregningstiden vokser mere end eksponentielt, når man tilføjer flere paller, og så kan selv de bedste computere ikke følge med. Så teoretisk er det muligt, men ud fra den hastighed som computeres regnekraft vokser med, vil det formentlig tage millioner af år, før vi kan håndtere nogle få ekstra objekter optimalt.”
Og har man så har at gøre med mere komplicerede figurer som fx klejner eller juletræsformede peberkager, kan man ifølge Mikkel Abrahamsen højst finde optimale løsninger for op til fire objekter i dag.
Uendeligt antal muligheder
Men hvorfor er det egentlig så svært? Mikkel Abrahamsen forklarer, at problemet svarer til at løse ligninger af grad fem eller højere og med mange ubekendte. Her er det kendt, at løsningen ikke altid kan skrives ned med de almindelige regneoperationer.
“Vores studie beviser, at problemet har en natur, som vi i matematikken kalder kontinuert – det betyder kort sagt, at man skal kende alle de koordinater, som småkagerne kan placeres i, og alle de vinkler, de kan roteres i,” siger Mikkel Abrahamsen.
Og fordi kombinationsmulighederne er uendeligt mange, kan det simpelthen ikke lade sig gøre at lave en liste over alle de placeringer, man skal prøve af for at finde den bedste pakning. I stedet må algoritmer, som løser pakningsproblemer optimalt, gå mere analytisk til værks, og det tager tid. Dette står i modsætning til mange andre kendte algoritmiske problemer, hvor man kan prøve en begrænset mængde af kombinationer af, før man finder den optimale. Det viser, at pakningsproblemerne er sværere end disse.
Så i praksis findes der ikke bedre løsninger på pakningsproblemer end dem, vi mennesker regner os frem til.
“Både industrien og småkagebagere må fortsat stille sig tilfreds med løsninger, som ikke er helt optimale, og hvile i visheden om, at vi mennesker trods alt stadig er bedre end computere til denne slags opgaver – indtil videre,” slutter Mikkel Abrahamsen.
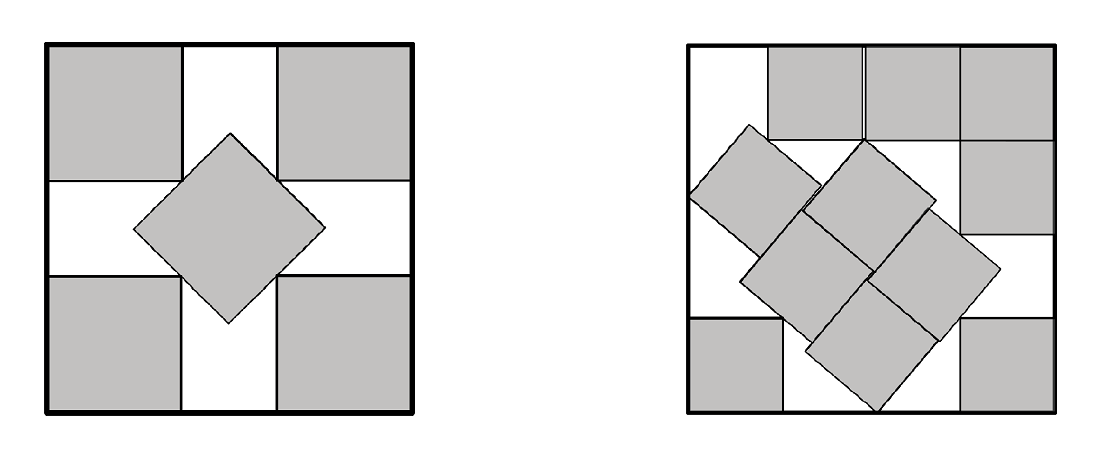
Venstre: Den optimale pakning af fem kvadratiske objekter. Højre: Den indtil videre mest optimale pakning, man kender af 11 kvadratiske objekter i en firkant.






